 【正解者】
|
１．ひろしさん |
Dec 4, 99 （解説がスゴイ ↓） |
|
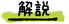
abcd
-) efgh
--------
48 とする。
ここでa-hは0,1,2,3,5,6,7,9のどれかであり、お互いに異なる整数である。
a キ e であるから、a=e+1....(1)
(1)より b の桁にくり下がるので10+b-f=0 (bの桁からくり下がり無し）
あるいは
10+b-1-f=0（bの桁からくり下がりあり）である。
ところが、10+b-f=0 => b+10=f を満たすb,fの組はありえない。
ゆえに10+b-1-f=0（くり下がりあり）である。
∴b + 9 = f
これを満たす組は (b, f ) = (0, 9)....(2)のみである。
一方、d-h=8あるいは10+d-h=8(くり下がり)
d-h=8を満たす組は(d,h)=(9,1)のみ。ところが、f=9であり、これはd キ h と
いう条件に反する。したがって、10+d-h=8(くり下がり)
∴h=d+2
これと(2)を満たす組は、(d,h) = (1,3), (3,5), (5,7)....(3)
c の桁は上の桁からくり下がり、下の桁へもくり下がるから
10+c-1-g=4
∴g = c+5
これと(2)を満たす組は(c, g) = (1, 6), (2, 7)....(4)
(4)のそれぞれの場合と(2)を満たす、(d, h) および (a, e)の
組み合わせを考えると
(b,c,f,g) = (0,1,9,6) の場合、(d, h) = (3, 5), (5, 7)
ここで、(1)よりa = e+1であるから、(d, h) = (3, 5)の組を満たす
(a, e) の組は存在しない。
∴(d, h) = (5, 7)
このとき(a, e) = (3, 2)
したがって、(a,b,c,d,e,f,g,h) = (3,0,1,5,2,9,6,7)
(b,c,f,g) = (0,2,9,7)の場合、
(d,h) = (1, 3), (3, 5)
ここで、(1)より a = e+1であるから、(d,h)=(3,5)の組を満たす
(a, e) の組は存在しない。
∴(d,h)=(1,3)
このとき (a, e) = (6, 5)
したがって、(a,b,c,d,e,f,g,h) = (6,0,2,1,5,9,7,3)
以上。
|
|
２．名古屋のガチャさん |
Dec 15, 99 |
|
”それぞれ二桁目（１００の位）には０と９しかありえないのと
上段４桁目（１の位）は２、６が入らないので（０，４をすでに
つかっているから）、組み合わせでわかりました。” |
|
